|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Проверка простой гипотезы относительно простой альтернативы
Лемма 4.1 (о вогнутости инфимума семейства вогнутых функций). Пусть функции  ,
, 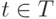 , определенные на выпуклом множестве X, вогнуты по x а этом множестве. Тогда нижняя огибающая этого семейства
, определенные на выпуклом множестве X, вогнуты по x а этом множестве. Тогда нижняя огибающая этого семейства
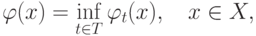 |
( 18.23) |
Доказательство. Пусть x1 и x2 есть две произвольные точки из множества X и точка
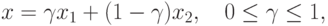 |
( 18.23) |
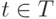 справедливо, что
справедливо, что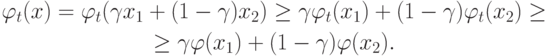 |
( 18.24) |
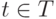 , то они должны
быть справедливы и для функции
, то они должны
быть справедливы и для функции 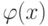 . Следовательно,
. Следовательно,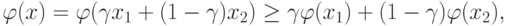
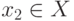 и
г
и
г 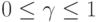 .
.Следствие 4.1. Функция байесовского риска 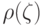 вогнута по
вогнута по  на интервале [0,1].
на интервале [0,1].
Доказательство В соответствии с определением (17.18), (17.19) и учитывая (18.21) и возможность задания любого байесовского критерия критической областью (18.17) из конечного набора (18.14), получаем, что
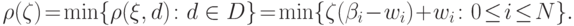 |
( 18.25) |
Поскольку линейные функции из правой части (18.25) являются вогнутыми, то в соответствии с утверждением леммы их нижняя огибающая также должна быть вогнутой.
Пример 4.3. Второй и третий столбцы табл. 4.4 представляют значения функций правдоподобия для некоторой схемы испытаний с четырьмя возможными исходами. При этом исходы занумерованы в соответствии с правилами (18.10)-(18.12) (см. четвертый столбец таблицы). Для заданного значения w=1,5 таблица содержит также граничные точки подынтервалов из (18.15), (18.16), вероятности ошибок первого и второго рода из (18.19), (18.20) и выражения для функций
![\rho_i(\zeta) = \zeta(\beta_i - w \alpha_i) + w \alpha_i,\,\zeta \in [0,1],](/sites/default/files/tex_cache/d8b16ffb3b7d7a6f4d8acb6da6573b5a.png) |
( 18.26) |
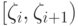 ,
, 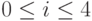 .
.| i | p1(zi) | p2(zi) | ci | 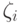 |
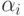 |
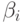 |
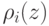 |
| 0 | - | - | 0 | 0 | 0 | 1 |  |
| 1 | 0,675 | 0,05 | 0,074 | 0,1 | 0,05 | 0,325 |  |
| 2 | 0,059 | 0,016 | 0,285 | 0,3 | 0,066 | 0,266 | 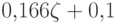 |
| 3 | 1,133 | 0,134 | 1 | 0,6 | 0,2 | 0,133 |  |
| 4 | 0,133 | 0,8 | 6 | 0,9 | 1 | 0 | 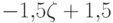 |
Представленная на рис. 4.4 функция 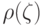 из (18.21), соответствующая данным из табл. 4.4,
иллюстрирует рассмотренные выше свойства байесовского риска.
из (18.21), соответствующая данным из табл. 4.4,
иллюстрирует рассмотренные выше свойства байесовского риска.
Определение 4.2 (наименее выгодного распределения).
Априорное распределение 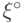 из (18.2),
при котором функция байесовского риска достигает максимального
значения
из (18.2),
при котором функция байесовского риска достигает максимального
значения
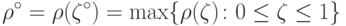 |
( 18.27) |
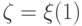 , называется наименее выгодным
распределением вероятностей для
состояний природы. Заметим, что точка
, называется наименее выгодным
распределением вероятностей для
состояний природы. Заметим, что точка 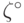 является внутренней точкой
интервала (0,1) и совпадает с одной из точек
является внутренней точкой
интервала (0,1) и совпадает с одной из точек 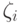 ,
, 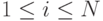 ,
поскольку функция
,
поскольку функция 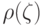 является вогнутой
и имеет, согласно (18.22), нулевые значения на
концах интервала [0,1] ; см. рис. 4.4.
является вогнутой
и имеет, согласно (18.22), нулевые значения на
концах интервала [0,1] ; см. рис. 4.4.

